Answer:
y = 2.56 10⁻² m
Step-by-step explanation:
The resolution of this telescope is given by the Rayleigh criterion, for the phenomenal diffraction the first minimum for a linear slit is in
a sin θ = λ
in general the angles are very small, so we approximate
sin θ = θ
we substitute
θ = λ / a
in the case of circular slits we must use polar coordinates, which introduces a numerical factor, leaving the equation
θ = 1.22
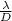
where D is the diameter of the circular opening
In this case they indicate the lens diameter D = 2.4 m, the observation distance r = 90.4 km = 90.4 10³ m
how angles are measured in radians
θ = y / r
we substitute
y / r = 1.22\frac{\lambda }{D}
y = 1.22 \frac{\lambda r }{D}
let's calculate
y =
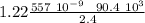
y = 2.56 10⁻² m
this is the minimum distance that can differentiate two objects on Earth