Question

A sample of 25 PCC studentsspent an average of $75 with a standard deviation of $17.50. Another sample of 20 ELAC studentsshowed that they spent an average of $89 with a standard deviation of $14.40. Assume that the amounts by all PCCand all ELAC students are normally distributed with equal but unknown population standard deviations.

Required:
Using 5% significance level and a formal hypothesis test can you conclude that the mean amount spent by all PCC students is less than the mean spent by all ELAC students?

Answer 1

Explanation:

Given that:

For PCC

The sample size
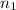`n_1` = 25

sample mean
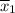`\overline x_1` = 75

standard deviation
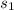`s_1` = 17.50

For ELAC

The sample size
`n_2` = 20

Sample mean
`\overline x_2 = 89`

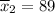
Standard deviation
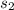`s_2` = 14.40

Significance level = 0.05

The null hypothesis:

`H_o : \mu_1 =\mu_2`

The alternative hypothesis;

`H_1 : \mu_1< \mu_2`

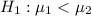
Since the population standard deviation are synonymous pooled standard deviation; Then:

`sp = \sqrt {\frac {(n_1-1)s_1^2)+(n_2-1)s_2^2 }{n_1+n_2-2}`

`sp = \sqrt {\frac {(25-1)17.50^2)+(20-1)14.40^2 }{25+20-2}`

`sp = 16.20`

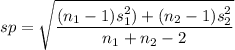
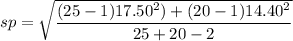
The test statistics can be computed as:

`t = \frac{\overline x_1 -\overline x_2}{sp * \sqrt{(1)/(n_1) + (1)/(n_2) }}`

`t = \frac{75-89}{16.20 * \sqrt{(1)/(25) + (1)/(20) }}`

`t = -2.88`

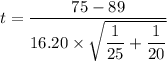
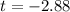
The p-value
`= P(t_(n_1+n_2-1) <t)`

`= P(t_(43) <-2.88)`

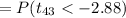
= 0.0031

Decision Rule: To reject the null hypothesis if the p-value is less than the significance level

Conclusion: There is sufficient evidence to conclude that the mean amount spent by all PCC students is less than the mean amount spent by all ELAC students.