Question

A communications system transmits a message. The probability that the message will be received is p. To be confident that a message is received at least once, the system transmits it n times. If a message is received, the receiver turns off and does not turn back on.

a. Assuming all transmissions are independent, what is the PMF of K, the number of times the pager receives the same message?
b. Assume p=0.8. What is the minimum value of n that produces a probability of 0.95 of receiving the message at least once?

Answer 1

Follows are the solution to the given points:

Step-by-step explanation:

In point a:

In the PMF of K, that pager receives its same message number of times, that is
`=\tiny \binom{n}{k}p^(k) (1-p)^(n-k)`

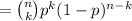
In point b:

The possibility of getting number of cultural at least once in x:

`\to 1-P(\text{not receiving it at all})\\\\\to 1-(0.2)x\\\\\to 1-(0.2)x>0.95\\\\\to (0.2)x<0.05 \\\\`

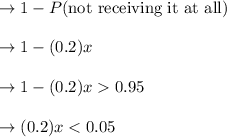
appling the
`\log`:

`\to x>0.25`

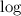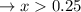
The value x is equal to 3.