Question

Suppose we want to prove the statement S(n): "If n ⥠2, the sum of the integers 2 through n is (n+2)(n-1)/2" by induction on n. To prove the inductive step, we can make use of the fact that 2+3+4+...+(n+1) = (2+3+4+...+n) + (n+1) Find, in the list below an equality that we may prove to conclude the inductive part.

a. If n ⥠3 then (n+2)(n-1)/2 + n + 1 = (n+3)(n)/2
b. If n ⥠1 then (n+2)(n-1)/2 + n + 1 = (n+3)(n)/2
c. If n ⥠2 then (n+2)(n-1)/2 + n + 1 = (n+3)(n)/2
d. If n ⥠1 then (n+2)(n-1)/2 + n + 1 = n(n+3)/2

Answer 1

The answer is "Choice c".

Step-by-step explanation:

Please find the complete question in the attached file.

To begin with, allow its principle of the numerically solving to be recognized, three stages are concerned.

1. Topic n=1

2. Suppose n to be true

3. Display n+1 it retains

We have LHS as 2+3+ for the third step now
`(n+1) = (2+3+.. \& n) + n+1`

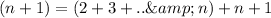
We can now replace the bracket of RHS by
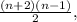`((n+2)(n-1))/(2),`as we assumed its valid for n in step 2

if we do that we get

`= ((n+2)(n-1))/(2+(n+1))\\\\= ((n^2-n+2n-2+2n+2))/(2)\\\\= ((n^2+3n))/(2)\\\\= (n(n+3))/(2)`