Question

The bonds in our model have a maturity close to zero; they just pay the current interest rate, i, as a flow over time. We could consider, instead, a discount bond, such as a U.S. Treasury Bill. This type of asset has no explicit interest payments (called coupons) but pays a principal of, say, $1000 at a fixed date in the future. A Bill with one- year maturity pays off one year from the issue date, and similarly for 3-month or 6-month Bills. Let PB be the price of a discount bond with one-year maturity and principal of $1000. a. Is PB greater than or less than $1000.

a. Is P^B greater than or less than $1000?
b. What is the one-year interest rate on these discount bonds?
c. If prises, what happens to the interest rate on these bonds?
d. Suppose that, instead of paying $1000 in one year, the bond pays $1000 in two years. What is the interest rate per year on this two-year discount bond?

Answer 1

Answer is explained in the explanation section below.

Step-by-step explanation:

Part a.

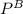`P^(B)` will be less than $1000.

Reason:
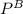`P^(B)` + interest = $1000, since interest >0 (Cannot be negative)

Hence,

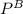`P^(B)` < $1000

Part b.

Assuming the amount of interest to be i,
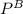`P^(B)` would be $1000 - I

Rate of interest would be:

($1000 - ($1000-i)) / ($1000 - i) = i / ($1000 - i)

Rate of interest = i / ($1000 - i)

Part c.

If
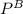`P^(B)` rises, the interest rate on these bonds would come down. Going back to a.
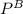`P^(B)` = $1000 - i, and if
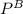`P^(B)` rises, it implies that i reduces, which means that rate of interest will be reduced.

Part d.

If $1000 is a payment two years later, it implies that i (refer to b.) is the interest for two years. Assuming annual compounding, let's calculate rate of interest as follows:

Interest for two year (i) = $1000 -
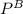`P^(B)` at the rate of i per year

=
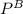`P^(B)` X i / 100 + (
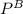`P^(B)` X (1+i/100))X i/100

We can solve for i to get annual rate of interest.