Question

Starting at 6 a.m. every morning, Matilda receives text messages on her cell phone from her mother, her best friend, and her brother according to three independent Poisson processes. Her mother texts Matilda on average once every hour. Her best friend sends a message once every 10 minutes, and she receives messages from her brother every 30 minutes.

A) Find the probability that by 7:30 a.m. Mary receives exactly four messages – two of her best friend and two of her mother.
B) With a chance of 75% a text message contains a typo independent of the sender. Find the probability that there are no typos in the text messages Matilda receives between 2 p.m. and 5 p.m.

Answer 1

a) 0.0013 = 0.13% probability that by 7:30 a.m. Mary receives exactly four messages – two of her best friend and two of her mother.

b)
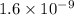`1.6 * 10^(-9)` probability that there are no typos in the text messages Matilda receives between 2 p.m. and 5 p.m.

Explanation:

Poisson distribution:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

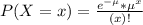
In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\mu` is the mean in the given interval.

A) Find the probability that by 7:30 a.m. Mary receives exactly four messages – two of her best friend and two of her mother.

Two from the best friend:

Her best friend sends a message once every 10 minutes.

From 6 to 7:30, there is an hour and a half, that is, 90 minutes, so the mean for her best friend is
`\mu = (90)/(10) = 9`

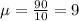
Two messages is P(X = 2). So

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 2) = (e^(-9)*9^(2))/((2)!) = 0.0050`

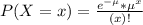
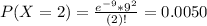
Two from the mother:

Message every hour = 60 minutes. So
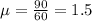`\mu = (90)/(60) = 1.5`. This is P(X = 2).

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 2) = (e^(-1.5)*1.5^(2))/((2)!) = 0.2510`

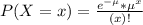
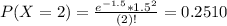
Two of her best friend and two of her mother:

Independent events, so the probability of both happening is the multiplication of their separate probabilities.

`p = 0.005*0.251 = 0.0013`

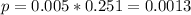
0.0013 = 0.13% probability that by 7:30 a.m. Mary receives exactly four messages – two of her best friend and two of her mother.

B) With a chance of 75% a text message contains a typo independent of the sender. Find the probability that there are no typos in the text messages Matilda receives between 2 p.m. and 5 p.m.

In 3 hours, she is expected to receive:

3*60/10 = 18 messages from her best friend.

3*60/60 = 3 messages from her mother.

3*60/30 = 6 messages from her brother.

In total, 27 messages.

75% probability of a typo, so
`\mu = 0.75*27 = 20.25`

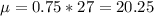
This is P(X = 0).

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 0) = (e^(-20.25)*20.25^(0))/((0)!) = 1.6 * 10^(-9)`

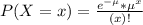
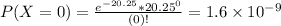
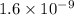`1.6 * 10^(-9)` probability that there are no typos in the text messages Matilda receives between 2 p.m. and 5 p.m.