Question

Find the numerical value of the log expression

Answer 1

By logarithmic properties and given logarithms, The numerical value of the logarithmic expression is - 12.

How to determine the numerical value of a logarithmic expression

We must look up to the numerical value of a logarithmic expression, this can be done on the basis on known logarithms and logarithm properties:

Logarithm of a product:

㏒ a · b = ㏒ a + ㏒ b

Logarithm of a division:

`\log (a)/(b) = \log a - \log b`

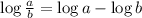
Logarithm of a power:

`\log a^c = c\cdot \log a`

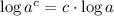
Now we proceed to find the numerical value of the logarithmic expression:

`\log (b^6 \cdot c^3)/(a^3)`

`\log b^6 \cdot c^3 - \log a^3`

`\log b^6 + \log c^3 - \log a^3`

`6 \cdot \log b + 3\cdot \log c - 3\cdot \log a`

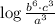
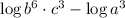
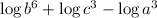
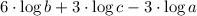
6 · (- 5) + 3 · 4 - 3 · (- 2)

- 30 + 12 + 6

- 12