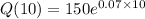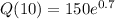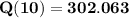Question

Given an initial quantity Q0=150 and a growth rate of 7% per unit time, give a formula for the quantity Q as a function of time t, and find the value of the quantity at t=10.

a) Assume the growth rate is not continuous. Round your answer for Q(10) to three decimal places.
Q(t)=
Q(10) =
b) Assume the growth rate is continuous. Round your answer for Q(10) to three decimal places.
Q(t)=
Q(10)=

Answer 1

Explanation:

From the given information:

(a)

Since growth quantity is not continuous

`Q(t) = 150 (1.07)^t`

For t = 10

`Q(10) = 150 (1.07)^(10)`

`\mathbf{Q(10) = 295.073}`

(b)

Here, for a continuous growth rate, the growth quantity can be computed in terms of initial quantity and the growth rate.

i.e.

`Q(t) = 150 e^(0.07t)`

At t = 10 for a continuous growth rate;

`Q(10) = 150 e^(0.07 * 10)`

`Q(10) = 150 e^(0.7)`

`\mathbf{Q(10) = 302.063}`