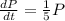Question

The population of a certain species of insect is given by a differentiable function P , where P(t) is the number of insects in the population, in millions, at time t , where t is measured in days. When the environmental conditions are right, the population increases with respect to time at a rate that is directly proportional to the population. Starting August 15, the conditions were favorable and the population began increasing. On August 20, five days later, there were an estimated 10 million insects and the population was increasing at a rate of 2 million insects per day. Which of the following is a differential equation that models this situation?

a. P=2(tâ5)+10
b. dP/dt=2/5t
c. dP/dt=1/5P
d. dP/dt=5P

Answer 1

Option C, dP/dt=1/5P

Explanation:

The change is population of insects is directly proportional to the rate of change of population

Hence,

`(dP)/(dt) \alpha P`

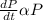
Or
`(dP)/(dt) = kP`

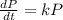
where K is the proportional constant

We will find the value of k

Keeping the given values of rate of change of population and population in above equation, we get -

`(2)/(10) = k\\k = (1)/(5)`

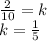
Hence,

`(dP)/(dt) = (1)/(5) P`