Question

Complete the following table.

Population Growth Rate, k Doubling Time, T
2.5% per year
Country A
Country B
50 years
Growth Rate, k Doubling Time,
T
Population
Country A
2.5% per year
Country B
% per year
(Round doubling time to the nearest whole number and round growth rate to the nearest tenth.)
years
50 years

Answer 1

The completed table can be presented as follows;

Population Growth Rate, k Doubling Time

Country A 2.5% per year 28 years

Country B 1.4% per year 50 years

The steps used to obtain the number of years and the growth rate are as follows;

The doubling time for country A can be obtained using the relationship

Let A represent the population of country A, when the population doubles, we get;

A×(1 + 0.025)ⁿ = 2·A

Where n is the number of years

(1 + 0.025)ⁿ = 2

n·ln(1 + 0.025) = ln(2)

`n = (\ln(2))/(\ln(1 + 0.025))`

`(\ln(2))/(\ln(1 + 0.025))\approx 28`

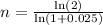
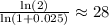
The number of years the population of country A doubles is 28 years

Number of years for population of country B to double = 50 years, therefore;

B × (1 + r)⁵⁰ = 2·B

(1 + r)⁵⁰ = 2

`\ln(1 + r) =(\ln(2))/(50)`

`1 + r = e^{(\ln(2))/(50)}`

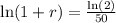
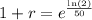
`e^{(\ln(2))/(50)} \approx 1.014`; The substitution property indicates that we get;

1 + r ≈ 1.014

r ≈ 0.014

0.014 = 1.4%

r ≈ 1.4%

The population growth rate is about 1.4%