Question

2. Dana is depositing money into her bank account. She deposits $60

each month. After 6 months she has $450.
a. What is the slope and what does it represent in this situation?
b. Write an equation to model the situation.
c. What is the y-intercept and what does it represent in this situation?

Answer 1

To solve this problem:

a. Slope and its representation:

The slope represents the rate at which Dana's bank account balance is changing per month. In this scenario, the slope can be calculated using the formula:

Slope=Change in y /Change in x

Slope= Change in x/Change in y

​

Dana deposits $60 each month for 6 months, and her balance increases from $0 to $450. So, the change in y (balance) is $450 - $0 = $450, and the change in x (number of months) is 6 - 0 = 6.

Slope=$450/6=$75

Therefore, the slope is $75, representing that Dana is depositing $75 more into her bank account every month.

b. Equation to model the situation:

The equation of a line in slope-intercept form is y=mx+b, where m is the slope, and b is the y-intercept.

Given the slope (m=$75) and knowing that after 6 months she has $450, we can use this information to find the y-intercept.

The equation becomes:

y=75x+b

Using the point (6, $450) where x=6 and y=$450:

$450 = 75 \times 6 + b

$450 = 450 + b

So, b=450−450=0

Therefore, the equation that models the situation is y=75x.

c. Y-intercept and its representation:

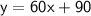
The y-intercept of the equation is 0, and in this context, it represents Dana's initial bank account balance before making any deposits, which is $0. The y-intercept is the starting point on the graph where the number of months (x) is 0, showing the initial amount in the account.

Answer 2

a. The slope (
`\sf m`) is 60, representing the rate of deposit per month.

b. The equation to model the situation is
`\sf y = 60x + 90`

c. The y-intercept
`\sf b` is 90, representing the initial amount of money in Dana's account.

Explanation:

Let's analyze the situation step by step:

a. Slope and its representation:

The slope
`\sf m` in this situation represents the rate at which Dana is depositing money each month.

Since she deposits 60 each month, the slope is
`\sf m = 60`.

b. Equation to model the situation:

The general form of a linear equation is
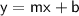`\sf y = mx + b`, where:

-
`\sf y` is the dependent variable (total amount of money in the account),

-
`\sf x` is the independent variable (number of months),

-
`\sf m` is the slope,

-
`\sf b` is the y-intercept.

In this situation, the equation becomes:

`\sf y = 60x + b`

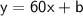
c. Y-intercept and its representation:

After 6 months
`\sf x = 6`.

Dana has 450 (
`\sf y = 450`. We can use this information to find the y-intercept
`\sf b`.

`\sf 450 = 60 * 6 + b`

`\sf 450 = 360 + b`

`\sf b = 90`

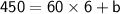
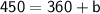
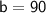
So, the y-intercept is 90, and in this situation, it represents the initial amount of money in Dana's account before any monthly deposits.

Summary:

a. The slope
`\sf m` is 60, representing the rate of deposit per month.

b. The equation to model the situation is
`\sf y = 60x + 90`.

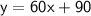c. The y-intercept
`\sf b` is 90, representing the initial amount of money in Dana's account.