Question

At Cascadia College, students need to take a 100 level Math and English courses plus an optional Philosophy course. In any quarter, the college needs to make available 4 less English sections than Math sections. In any quarter student demand for the optional Philosophy course is half as many sections as English sections. Available classrooms limit the total sections of all three courses to 44

Given these constraints how many sections of each course should the college make available each quarter to meet demand?
Math sections =
English sections =
Philosophy sections =

Answer 1

Math sections = 20

English sections = 16

Philosophy sections = 8

Explanation:

This question can be solved using a system of equations.

I am going to say that:

x is the number of Math sections.

y is the number of English sections.

z is the number of Philosophy sections.

Available classrooms limit the total sections of all three courses to 44.

This means that
`x + y + z = 44`

4 less English sections than Math sections.

This means that
`y = x - 4`

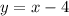
In any quarter student demand for the optional Philosophy course is half as many sections as English sections.

This means that
`z = (y)/(2) = (x - 4)/(2)`

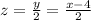
Finding the number of Math sections:

We have both y and z as functions of x. So

`x + y + z = 44`

`x + x - 4 + (x-4)/(2) = 44`

`2x + (x-4)/(2) = 48`

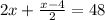
Multiplying everything by 2

`4x + x - 4 = 96`

`5x = 100`

`x = (100)/(5)`

`x = 20`

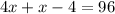
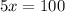
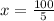
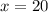
Then

`y = x - 4 = 20 - 4 = 16`

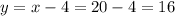
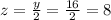`z = (y)/(2) = (16)/(2) = 8`. So

Math sections = 20

English sections = 16

Philosophy sections = 8