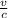Answer:
a) f ’’ = f₀
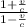 , b) Δf = 2 f₀
, b) Δf = 2 f₀
Step-by-step explanation:
a) This is a Doppler effect exercise, which we must solve in two parts in the first the emitter is fixed and in the second when the sound is reflected the emitter is mobile.
Let's look for the frequency (f ’) that the mobile aorta receives, the blood is leaving the aorta or is moving towards the source
f ’= fo
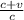
This sound wave is reflected by the blood that becomes the emitter, mobile and the receiver is fixed.
f ’’ = f’
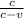
where c represents the sound velocity in stationary blood
therefore the received frequency is
f ’’ = f₀
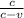
let's simplify the expression
f ’’ = f₀ \frac{c+v}{c-v}
f ’’ = f₀
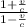
b) At the low speed limit v <c, we can expand the quantity
(1 -x)ⁿ = 1 - x + n (n-1) x² + ...
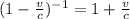
f ’’ = fo
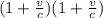
f ’’ = fo
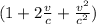
leave the linear term
f ’’ = f₀ + f₀ 2
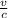
the sound difference
f ’’ -f₀ = 2f₀ v/c
Δf = 2 f₀