Question

The electric field between two parallel plates is uniform, with magnitude 646 N/C. A proton is held stationary at the positive plate, and an electron is held stationary at the negative plate. The plate separation is 4.26 cm. At the same moment, both particles are released.

Required:
Determine the distance from the positive plate at which the two pass each other.

Answer 1

The distance from the positive plate at which the two pass each other is 0.0023 cm.

Step-by-step explanation:

We need to find the acceleration of each particle first. Let's use the electric force equation.

`F=Eq`

`ma=Eq`

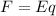
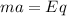
For the proton

`m_(p)a_(p)=Eq_(p)`

`a_(p)=(Eq_(p))/(m_(p))`

`a_(p)=(646*1.6*10^(-19))/(1.67*10^(−27))`

`a_(p)=6.19*10^(10)\: m/s^(2)`

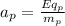
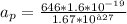
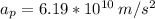
For the electron

`m_(e)a_(e)=Eq_(e)`

`a_(e)=(Eq_(e))/(m_(e))`

`a_(e)=(646*1.6*10^(-19))/(9.1*10^(−31))`

`a_(e)=1.14*10^(14)\: m/s^(2)`

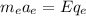
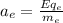
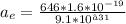
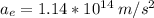
Now we know that the plate separation is 4.26 cm or 0.0426 m. The travel distance of the proton plus the travel distance of the electron is 0.0426 m.

`x_(p)+x_(e)=0.0426`

Both of them have an initial speed equal to zero. So we have:

`(1)/(2)a_(p)t^(2)+(1)/(2)a_(e)t^(2)=0.0426`

`t^(2)(a_(p)+a_(e))=2*0.0426`

`t^(2)=(2*0.0426)/(a_(p)+a_(e))`

`t=\sqrt{(2*0.0426)/(6.19*10^(10)+1.14*10^(14))}`

`t=2.73*10^(-8)\: s`

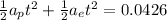
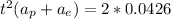
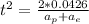
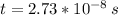
With this time we can find the distance from the positive plate (x(p)).

`x_(p)=(1)/(2)a_(p)t^(2)`

`x_(p)=(1)/(2)6.19*10^(10)*(2.73*10^(-8))^(2)`

`x_(p)=0.0023\: cm`

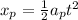
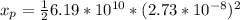
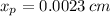
Therefore, the distance from the positive plate at which the two pass each other is 0.0023 cm.

I hope it helps you!