Answer:
29.8–34.2 hours
Explanation:
Empirical Rule:
The Empirical Rule states that, for a normally distributed random variable:
68% of the measures are within 1 standard deviation of the mean.
95% of the measures are within 2 standard deviation of the mean.
99.7% of the measures are within 3 standard deviations of the mean.
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean
 and standard deviation
and standard deviation
 , the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
 and standard deviation
and standard deviation
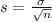 .
.
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
Population:
Mean of 32, standard deviation of 2.5.
Sample:
Sample of 5, so
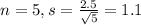
There is about a 95% probability that the sample mean will fall in which interval?
Within 2 standard deviations of the mean. So
32 - 2*1.1 = 32 - 2.2 = 29.8
32 + 2*1.1 = 32 + 2.2 = 34.2 hours