Question

When an accident investigator arrives at a scene. Here are some questions she is able to

answer by just knowing a few facts about the vehicles involved. The coefficient of friction
between a car's tires and the dry pavement is 0.55. The car's mass is 725 kg. It was traveling at
a constant velocity of 30.0 m/s when the driver slammed on the brakes and the wheels locked
up and it began to slide.
A) What is the weight of the car?
B) What is the force of friction
acting on the car?
C) What is the acceleration of the car?
D) How long does it take to stop the
car?
E) What was the distance the car skidded?

Answer 1

A) The weight of the car is approximately 7100 N.

B) The force of friction acting on the car is approximately 3895 N.

C) The acceleration of the car is approximately -5.38 m/s².

D) It takes approximately 5.57 seconds to stop the car.

E) The distance the car skidded is approximately 83.5 meters.

Step-by-step explanation:

To determine the weight of the car (A), we use the formula
`\( \text{Weight} = \text{mass} * \text{gravity} \)`, where gravity is approximately
`\( 9.8 \, \text{m/s}^2 \)`.

The force of friction (B) can be calculated using
`\( \text{Force of friction} = \text{friction coefficient} * \text{Weight} \)`.

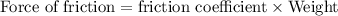The acceleration (C) is found using
`\( \text{Acceleration} = \frac{\text{Force of friction}}{\text{mass}} \)\\`.

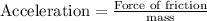The time to stop the car (D) is determined using the kinematic equation
`\( \text{time} = \frac{\text{final velocity} - \text{initial velocity}}{\text{acceleration}} \)`.

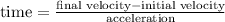Finally, the distance (E) is calculated using
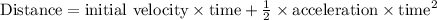`\( \text{Distance} = \text{initial velocity} * \text{time} + (1)/(2) * \text{acceleration} * \text{time}^2 \)`.