Question

An ideal spring is lying horizontally on a frictionless surface. One end of the spring is attached to a wall. The other end is attached to a moveable block that has a mass of 5 kg. The block is pulled so that the spring stretches from its equilibrium position by 0.65 m. Then the block is released (from rest), and as a result the system oscillates with a frequency of 0.40 Hz (that's 0.40 rev/sec) Find:

a) the acceleratiuon of the block when the spring is stretched by 0.28 m.
b) the maximum force magnitude exerted by the spring on the block.
c) the oscillation frequency of a 2.5 kg blcok under the same circumstances (i.e. with the same spring and initial displacement).

Answer 1

a) a = - 1.76 m / s², b) F = 20.5 N, c) w = 3.55 rad / s

Step-by-step explanation:

a) a simple harmonic motion is described by the expression

x = A cos (wt + Ф)

in this case they give us the frequency

w = 2π f

w = 2π 0.40

w = 2.51 rad / s

as the maximum elongation is 0.65 m this corresponds to the amplitude of the movement

A = 0.65 m

to find the phase constant (Ф) we use the initial condition that for t = 0 v = 0 and x = A, we substitute

A = A cos (0+ Ф)

cos Ф = 1

Ф = 0

the resulting equation is

x = 0.65 cos (2.51 t)

Let's find the time it takes to get to x = 0.28 m

0.28 = 0.65 cos 2.51 t

2.51 t = cos-1 (0.28 / 0.65)

remember angles are in radians

t = 1.1254 / 2.51

t = 0.448 s

the acceleration is

`a = (dv)/(dt) = (d^2x)/(dt^2)`

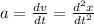
a = -A w² cos wt

we subtitle

a = - 0.65 2.51² cos (2.51 0.448)

a = - 1.76 m / s²

b) the maximum acceleration occurs when the cosine is ±1

a = A w²

a = 0.65 2.51²

a = 4.10 m / s²

Let's use Newton's second law

F = m a

F = 5 4.1

F = 20.5 N

c) The angular velocity is given by

w² = k / m

let's find the spring constant

k = m w²

k = 5 2.51²

k = 31.5 N / m

therefore if the block is exchanged for another with mass m'= 2.5 kg

w = √(31.5 / 2.5)

w = 3.55 rad / s