Question

A given field mouse population satisfies the differential equation dp/dt=.4p-450 where p is the number of mice and t is the time in months.

(a) Find the time at which the population becomes extinct if p(0)=1075
Round your answer to two decimal places in months.
(b) Find the initial population Po if the population is to become extinct in 1 year.
Round your answer to the nearest integer.
Po= mice

Answer 1

a) 7.78 months

b) 1116

Explanation:

Given -

`(dP)/(dt) = 0.4p-450`

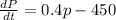
Integrating the above equation with respect to time, we get -

`\int\ (dP)/(0.4p-450) = \int\ dt\\`

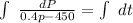
let us define new variable x

`x = 0.4p - 450 \\dx = 0.4 dy`

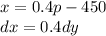
substituting these values in above integral equation, we get -

`(1)/(0.4) \int\ (dx)/(x) = \int\ dt\\ln x = 0.4 t + C\\x = ce^(0.4t)`

`P (t) = (C)/(0.4) e^(0.4t) +1125\\`

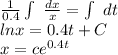
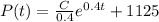
at t = 0, P (0) = 1075, using this condition, we get -

`(c)/(0.4) = -50\\P(t) = 50 e^(0.4t) +1125 \\t = 7.78\\P(0) = 1125 - (1125)/(e^(4.8)) = 1116`