Answer:
a) The rocket reaches a maximum height of 737.577 meters.
b) The rocket will come crashing down approximately 17.655 seconds after engine failure.
Step-by-step explanation:
a) Let suppose that rocket accelerates uniformly in the two stages. First, rocket is accelerates due to engine and second, it is decelerated by gravity.
1st Stage - Engine
Given that initial velocity, acceleration and travelled distance are known, we determine final velocity (
 ), measured in meters per second, by using this kinematic equation:
), measured in meters per second, by using this kinematic equation:
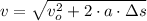 (1)
(1)
Where:
 - Acceleration, measured in meters per square second.
- Acceleration, measured in meters per square second.
 - Travelled distance, measured in meters.
- Travelled distance, measured in meters.
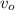 - Initial velocity, measured in meters per second.
- Initial velocity, measured in meters per second.
If we know that
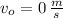 ,
,
 and
and
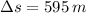 , the final velocity of the rocket is:
, the final velocity of the rocket is:


The time associated with this launch (
 ), measured in seconds, is:
), measured in seconds, is:
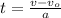
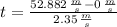
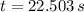
2nd Stage - Gravity
The rocket reaches its maximum height when final velocity is zero:
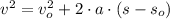 (2)
(2)
Where:
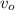 - Initial speed, measured in meters per second.
- Initial speed, measured in meters per second.
 - Final speed, measured in meters per second.
- Final speed, measured in meters per second.
 - Gravitational acceleration, measured in meters per square second.
- Gravitational acceleration, measured in meters per square second.
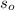 - Initial height, measured in meters.
- Initial height, measured in meters.
 - Final height, measured in meters.
- Final height, measured in meters.
If we know that
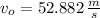 ,
,
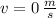 ,
,
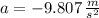 and
and
 , then the maximum height reached by the rocket is:
, then the maximum height reached by the rocket is:
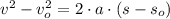
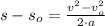
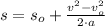
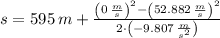
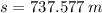
The rocket reaches a maximum height of 737.577 meters.
b) The time needed for the rocket to crash down to the launch pad is determined by the following kinematic equation:
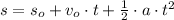 (2)
(2)
Where:
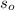 - Initial height, measured in meters.
- Initial height, measured in meters.
 - Final height, measured in meters.
- Final height, measured in meters.
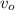 - Initial speed, measured in meters per second.
- Initial speed, measured in meters per second.
 - Gravitational acceleration, measured in meters per square second.
- Gravitational acceleration, measured in meters per square second.
 - Time, measured in seconds.
- Time, measured in seconds.
If we know that
 ,
,
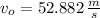 ,
,
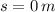 and
and
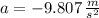 , then the time needed by the rocket is:
, then the time needed by the rocket is:
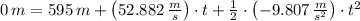
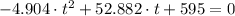
Then, we solve this polynomial by Quadratic Formula:
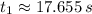 ,
,
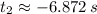
Only the first root is solution that is physically reasonable. Hence, the rocket will come crashing down approximately 17.655 seconds after engine failure.