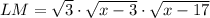Question

This is urgent my deadline is in a few hours.

Answer 1

The missing length
`$LM$` is equal to
`$√(3) \cdot √(x - 3) \cdot √(x - 17)$`

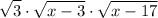
Here is a diagram of the triangle, with the lengths labeled:

The Pythagorean Theorem states that:

`LM^2 = (x+3)^2 + (2x-12)^2`

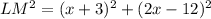
Expanding the squares, we get:

`LM^2 = x^2 + 6x + 9 + 4x^2 - 48x + 144`

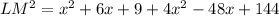
Combining like terms, we get:

`LM^2 = 3x^2 - 54x + 153`

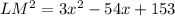
Taking the square root of both sides, we get:

`LM = √(3x^2 - 54x + 153)`

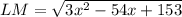
We can simplify the radical by factoring the expression under the radical. We notice that all of the terms in the expression have a common factor of
`$3$`, so we can pull it out:

`LM = √(3(x^2 - 18x + 51))`

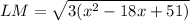
We can then factor the expression
`$x^2 - 18x + 51$` using the sum-product pattern:

`x^2 - 18x + 51 = (x - 3)(x - 17)`

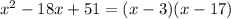
Substituting this into the expression for
`$LM$`, we get:

`LM = √(3(x - 3)(x - 17))`

Finally, we can simplify the radical by taking the square root of each term:

`LM = √(3) \cdot √(x - 3) \cdot √(x - 17)`