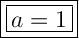Question

The point C(-1,-3) and D(2a,0) are in a plane. Given that |CD| = 3✓2 units, find the positive value of a.​

Answer 1

a = 1

Explanation:

The distance between two points in a plane can be found using the distance formula:

`\boxed{\begin{array}{l}\underline{\sf Distance \;Formula}\\\\d=√((x_2-x_1)^2+(y_2-y_1)^2)\\\\\textsf{where:}\\ \phantom{ww}\bullet\;\;d\;\textsf{is the distance between two points.} \\\phantom{ww}\bullet\;\;\textsf{$(x_1,y_1)$ and $(x_2,y_2)$ are the two points.}\end{array}}`

In this case, the two points are C(-1, -3) and D(2a, 0), and the distance between them is 3√2 units.

To find the value of a of point D, we can substitute the given values into the distance formula, then solve for a.

`|CD|=√((x_D-x_C)^2+(y_D-y_C)^2)`

`3√(2)=√((2a-(-1))^2+(0-(-3))^2)`

`3√(2)=√((2a+1)^2+(0+3)^2)`

`3√(2)=√((2a+1)^2+(3)^2)`

`3√(2)=√(4a^2+4a+1+9)`

`3√(2)=√(4a^2+4a+10)`

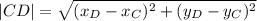
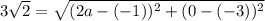
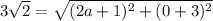
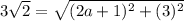
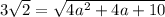
Square both sides of the equation:

`18=4a^2+4a+10`

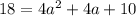
Subtract 18 from both sides of the equation:

`4a^2+4a-8=0`

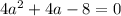
Factor out 4:

`4(a^2+a-2)=0`

`a^2+a-2=0`

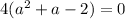
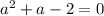
Now, solve the quadratic equation:

`a^2+2a-a-2=0`

`a(a+2)-1(a+2)=0`

`(a-1)(a+2)=0`

`a-1=0 \implies a=1`

`a+2=0 \implies a=-2`

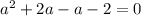
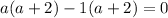
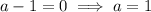
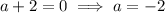
Therefore, the two possible values of a are a = 1 and a = -2.

So, the positive value of a is:

`\Large\boxed{\boxed{a=1}}`