Question

Need help guy! Thanks!

Answer 1

The expression that is equivalent to
`(2^(-5))/(2^(-1))$is $2^(-4)$`.

The question asks which expression is equivalent to
`$(2^(-5))/(2^(-1))$`. This means that we need to find an expression that has the same value as
`$(2^(-5))/(2^(-1))$`.

We can simplify the expression
`$(2^(-5))/(2^(-1))$` using the following rule of exponents:
`$(a^m)/(a^n) = a^(m-n)$`. Applying this rule, we get:

`(2^(-5))/(2^(-1)) = 2^(-5-(-1)) = 2^(-4)`

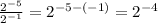
The four answer choices are
`2^6$,$2^(-4)$, $2^(-6)$, and $2^(-5)$`

The only answer choice that is equivalent to
`2^(-4)$ is 2^(-4)$`. Therefore, the correct answer is
`$2^(-4)$`.