Answer:
The answer is below
Explanation:
In preparation for the upcoming school year, a teacher looks at raw test scores on the statewide standardized test for the students in her class. Instead of looking at the scores relative to the norms in the state, the teacher wants to understand the scores relative to the students who will be in the class. To do so, she decides to convert the test scores into z-scores relative to the mean and standard deviation of the students in the class. The mean test score in her upcoming class is 202, and the standard deviation is 38.2. The following are the scores for some (not all) of her students. Complete the table using the dropdown menus. The teacher wants to identify those students who may need extra challenge or extra help. As a first cut, she decides to look at students who have z-scores above z = 2.00 or below z = -2.00. Identify the test score corresponding to each of the following z-scores. Round to the nearest whole number. For z = 2.00, test score = .For z - -2.00, test score = .
Solution:
The z score is a used in statistics to determine by how many standard deviations the raw score is above or below the mean. The z score is given by:
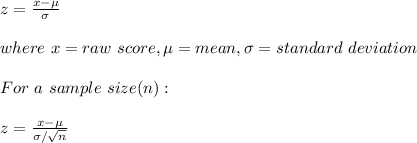
Given that μ = 202, σ = 38.2
i) for student B, x = 199. Hence:

ii) for student D, x = 222. Hence:
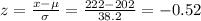
iii) for student F, x = 172. Hence:
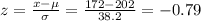
iv) for student H, x = 215. Hence:
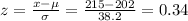
For z = 2.00, the test score x is:
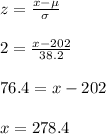
For z = -2.00, the test score x is:
