The function
 undergoes transformations to create function g(x). A vertical stretch by a factor of 3 corresponds to
undergoes transformations to create function g(x). A vertical stretch by a factor of 3 corresponds to
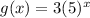 , and a vertical compression by 1/3 corresponds to
, and a vertical compression by 1/3 corresponds to
 .
.
To identify how the function
 is transformed to create function g(x), let's match each transformation with its description:
is transformed to create function g(x), let's match each transformation with its description:
A. **Vertical stretch of a factor of 3:** This corresponds to multiplying the entire function by 3 outside the exponent.
- Match:
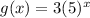
B. **Vertical compression of a factor of 1/3:** This corresponds to multiplying the entire function by
 outside the exponent.
outside the exponent.
- Match:

C. **Horizontal stretch of a factor of 3:** This corresponds to replacing
 inside the exponent.
inside the exponent.
- Match:
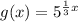
D. **Horizontal compression of a factor of 1/3:** This corresponds to replacing x with 3x inside the exponent.
- Match:
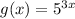
So, the correct matches are:
1. A -
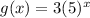
2. B -

3. C -
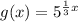
4. D -
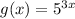
The probable question may be:
Consider this function.
f(x) = 5ˣ
How is function f transformed to create function g?
Match each transformation of function f with its description.
A. vertical stretch of a factor of 3
B. vertical compression of a factor of 1/3
C. horizontal stretch of a factor of 3
D. horizontal compression of a factor of 1/3
Options:
1. g(x) = 3(5)ˣ
2. g(x) = 1/3(5)ˣ
3. g(x) = 5^1/3x
4. g(x) = 5³ˣ