Question

Triangle RPQ is shown

Answer 1

To prove x = 35, Nora states and reasons that ST is parallel to QR, angles are congruent, triangles are similar, and then uses the ratio of corresponding sides in similar triangles to establish the equation
`\((28)/(x) = (40)/(x+15)\).`

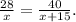
To prove that if segment ST is parallel to segment RQ, then x = 35, Nora can use the following statements and reasons:

1. Statement: ST is parallel to QR

Reason: Given (a).

2. Statement: Angle QRT is congruent to angle STP

Reason: Corresponding angles formed by parallel lines and their transversal are congruent (b).

3. Statement: Angle SPT is congruent to angle QPR

Reason: Reflexive property of angles (c).

4. Statement: Triangle SPT is similar to triangle QPR

Reason: Angle-Angle similarity postulate (d).

5. Statement:
`\((28)/(x) = (40)/(x + 15)\)`

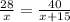
Reason: Corresponding sides of similar triangles are in proportion (e).

Now, explain why statement 5 is valid:

Since triangles SPT and QPR are similar (Statement 4), the ratio of corresponding sides is constant. Therefore, the ratio of PS to PT in triangle SPT must be equal to the ratio of QS to QR in triangle QPR:

`\[ (28)/(x) = (40)/(x + 15) \]`

This equation represents the proportionality of corresponding sides, providing a valid explanation for Nora's statement 5.