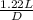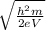Question

A Typical operating voltage of an electron microscope is 50 kV. A Typical experimental operating voltage range of a Scanning electron microscope is 1kV to 30kV. Higher voltages can penetrate and causes deformation on the sample. Lets assume it operates at 10kV. (i)What is the smallest distance that it could possibly resolve

Answer 1

y =
`(1.22L)/(D)`
`\sqrt{(h^2 m)/(2eV) }`

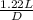
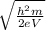
Step-by-step explanation:

Let's solve this exercise in parts. Let's start by finding the wavelength of the electrons accelerated to v = 10 103 V, let's use the DeBroglie relation

λ=
`(h)/(p) = (h)/(mv)`

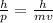
Let's use conservation of energy for speed

starting point

Em₀ = U = e V

final point

Em_f = K = ½ m v²

Em₀ = Em_f

eV = ½ m v²

v =
`\sqrt{(2eV)/(m) }`

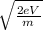
we substitute

λ=
`\sqrt{ (h^2 m)/(2eV)}`

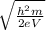
the diffraction phenomenon determines the minimum resolution, for this we find the first zero of the spectrum

a sin θ = m λ

first zero occurs at m = 1, also these experiments are performed at very small angles

sin θ = θ

θ = λ / a

This expression is valid for linear slits, in the microscope the slits are circular, when solving the polar coordinates we obtain

θ = 1.22 λ / D

where D is the diameter of the opening

we substitute

θ =
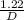`(1.22)/(D)` \sqrt{ \frac{h^2 m}{2eV}}

this is the minimum angle that can be seen, if the distance is desired suppose that the distance of the microscope is L, as the angles are measured in radians

θ = y / L

when substituting

where y is the minimum distance that can be resolved for this acceleration voltage

y =
`(1.22L)/(D)`
`\sqrt{(h^2 m)/(2eV) }`