Question

Hi, can someone help me with this practice question.

Answer 1

a. Slope = 3, y-intercept = 1 (or 5), type of solution = No solution (parallel lines).

b. Slope = 2 and -2, y-intercepts = 2 and 4, type of solution = One solution.

c. Slope and y-intercepts are not applicable (as the lines are identical), type of solution = Infinitely many solutions.

Let's analyze each system of equations:

a.
`\( \begin{cases} y = 3x + 1 \\ y = 3x + 5 \end{cases} \)`

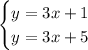
In this case, both equations have the same slope (3) but different y-intercepts (1 and 5). The lines are parallel and will never intersect, indicating no solution.

b.
`\( \begin{cases} y = 2x + 2 \\ y = -2x + 4 \end{cases} \)`

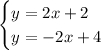
These two lines have different slopes (2 and -2) and different y-intercepts (2 and 4). The lines are not parallel, and they intersect at a single point. Thus, there is one solution.

c.
`\( \begin{cases} x - 2y = 1 \\ 2x - 4y = 2 \end{cases} \)`

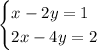
To determine the type of solution, we can check if the two equations are dependent or independent. If they are dependent and represent the same line, there are infinitely many solutions. If they are independent and intersect at a point, there is one solution.

Let's multiply the first equation by 2 to make the coefficients of y the same:

`\[ \begin{cases} 2x - 4y = 2 \\ 2x - 4y = 2 \end{cases} \]`

Now, the two equations are identical, representing the same line. Therefore, there are infinitely many solutions.