Question

4. Given the two equations, which has a greater

rate of change: f(x) of g(x)?
-4-3-2-1
x

Answer 1

The line g(x) has a greater rate of change compared to f(x), as evidenced by their respective slopes. g(x) has a slope of
`\((2)/(3)\)`, which is larger than f(x)'s slope of
`\((1)/(4)\).`

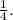
To determine which line, f(x) or g(x), has a greater rate of change, we can compare the slopes of the two lines.

The slope of a line passing through two points
`\((x_1, y_1)\) and \((x_2, y_2)\)` is given by the formula:

`\[ \text{Slope} = (y_2 - y_1)/(x_2 - x_1) \]`

Let's calculate the slopes for both lines:

For line f(x), passing through points (-4,-2), (0,-1), (4,0):

`\[ \text{Slope}_(f) = (-1 - (-2))/(0 - (-4)) = (1)/(4) \]`

For line g(x), passing through points (-3,-4), (0,-2), (3,0), (6,2):

`\[ \text{Slope}_(g) = (-2 - (-4))/(0 - (-3)) = (2)/(3) \]`

Comparing the slopes, we find that g(x) has a greater rate of change, as its slope (
`\((2)/(3)\)`) is larger than the slope of f(x) (
`\((1)/(4)\)`).