Question

If you’re able to help me i would appreciate it a lot! I have asked a lot of tutors but they cancelled on me . If you can please answer this for me and help me worth the other parts that’d mean so much !

( i need to fill in the blanks for this portion )

(I don’t know what I filed out was correct but I doubt it )

Answer 1

Part 1: Calculated sum of squares for residuals for lines y = -x + 11 and y = -0.5x + 8. Line y = -0.5x + 8 has a smaller sum, indicating a better fit.

Part 2: Equation for the line of best fit: y = -0.5x + 8. Slope represents average decrease in incorrect answers, y-intercept predicts initial incorrect answers.

Part 3: Line y = -0.5x + 8 represents data well, with minimized residuals and visually fitting the scatter plot.

Part 1:

To find the sum of the squares for the residuals for each line, we need to calculate the residuals (the differences between the actual values and the predicted values), square them, and then sum them up.

For the line y = -x + 11:

- Residuals:
`\(8 - (-2 + 11) = -1\), \(9 - (-4 + 11) = -2\), \(1 - (-6 + 11) = 4\), \(4 - (-9 + 11) = 6\)`

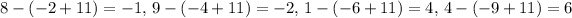
- Sum of the squares for the residuals:
`\(1^2 + 2^2 + 4^2 + 6^2 = 1 + 4 + 16 + 36 = 57\)`

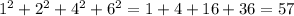
For the line y = -0.5x + 8:

- Residuals:
`\(8 - (-1 + 8) = -1\), \(9 - (-2 + 8) = -1\), \(1 - (-4 + 8) = 5\), \(4 - (-5 + 8) = 1\)`

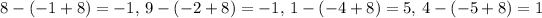
- Sum of the squares for the residuals:
`\(1^2 + 1^2 + 5^2 + 1^2 = 1 + 1 + 25 + 1 = 28\)`

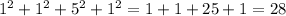
Comparing the sum of the squares for the residuals, a smaller value indicates a better fit. Therefore, the line y = -0.5x + 8 is a better fit.

Part 2:

The equation for the line of best fit is y = -0.5x + 8. In this equation:

- The slope (-0.5) represents the average decrease in incorrect answers for each additional hour spent on homework.

- The y-intercept (8) represents the predicted number of incorrect answers when no time is spent on homework.

To predict the number of incorrect answers for 5 hours of study (x = 5):

`\[ y = -0.5 * 5 + 8 = 5.5 \]`

Therefore, the predicted number of incorrect answers for 5 hours of study is 5.5.

Part 3:

To evaluate how well the line of best fit represents the data, we can consider factors such as the residuals, the sum of the squares for the residuals, and the visual fit on a scatter plot. If the residuals are small and the sum of the squares for the residuals is minimized, the line is a good fit. Additionally, visually inspecting the scatter plot can provide insights into the line's appropriateness for representing the data accurately.

Using y = -x + 11:

- When x = 2, y = -2 + 11 = 9.

- When x = 4, y = -4 + 11 = 7.

- When x = 8, y = -8 + 11 = 3.

- When x = 10, y = -10 + 11 = 1.

These values represent the predicted number of incorrect answers based on the given equation.