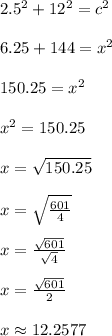Exact answer:
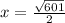
Approximate answer:
====================================================
How to find the answer:
Focus on the largest triangle. It appears to be a right triangle. If so, then we can use the pythagorean theorem to get the following:
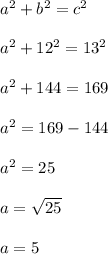
The horizontal leg of the largest right triangle is 5 units long.
The identical single tickmarks tell us that the horizontal leg is cut into two smaller pieces of equal length.
Each smaller piece is 5/2 = 2.5 units long.
------------------------------
Now focus on the smaller skinny right triangle with legs a = 2.5, b = 12 and hypotenuse c = x.
Use the pythagorean theorem again to find the hypotenuse x.