The surface area of a sphere with a radius of 3.6 feet is
 . Calculated using the formula
. Calculated using the formula
 , where r is the radius and
, where r is the radius and
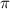 is approximated as 3.14, rounding to the nearest hundredth for precision.
is approximated as 3.14, rounding to the nearest hundredth for precision.
To find the surface area (A) of a sphere, we use the formula
 , where r is the radius. Given a radius of 3.6 feet, substitute this value into the formula:
, where r is the radius. Given a radius of 3.6 feet, substitute this value into the formula:
![\[ A = 4 * 3.14 * (3.6)^2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/89hwattzryv0zma395dvc81vni9hwrbe6g.png)
Calculate:
![\[ A = 4 * 3.14 * 12.96 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/vcualk2p3we6akijkclvqsbhbg3yub5nh4.png)
![\[ A = 162.24 \, \text{ft}^2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/pmhwooddyrwn2y39zvk69xunq6c0zcoesk.png)
Therefore, the surface area of the sphere is
 . The use of 3.14 for
. The use of 3.14 for
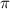 and rounding the answer to the nearest hundredth ensures the precision of the result. The calculation involves squaring the radius, multiplying by
and rounding the answer to the nearest hundredth ensures the precision of the result. The calculation involves squaring the radius, multiplying by
 , and performing the necessary arithmetic.
, and performing the necessary arithmetic.