Question

Find the surface area of a sphere with a diameter of 40 inches. Leave your answer in terms of pi. (1 point)

The surface area is blank in^2

Answer 1

The surface area of a sphere with a diameter of 40 inches is
`\(1600\pi \, \text{in}^2\)`. The calculation involves finding the radius, applying the formula
`\(A = 4\pi r^2\)`, resulting in an exact expression in terms of
`\(\pi\).`

To find the surface area of a sphere, we use the formula
`\(A = 4\pi r^2\)`, where r is the radius. Since the diameter is given, we can find the radius by dividing the diameter by 2.

Given a diameter of 40 inches, the radius (r) is 40/2 = 20 inches. Now substitute this value into the formula:

`\[ A = 4\pi (20)^2 \]`

Simplifying,

`\[ A = 4\pi * 400 \]`

`\[ A = 1600\pi \]`

Therefore, the surface area of the sphere is
`\(1600\pi \, \text{in}^2\)`. This is the exact expression in terms of
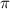`\(\pi\)` since the value of
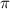`\(\pi\)` is irrational, and leaving it in this form provides a more accurate representation of the surface area.