Question

22 OXYZ is a parallelogram. OX = a OY = b R P P is the point on OX such that OP: PX=1:2 R is the point on OY such that OR: RY= 1:3 Work out, in its simplest form, the ratio ZP: ZR You must show all your working. X Y​

Answer 1

In the parallelogram OXYZ, with OX = a and OY = b, points P and R on OX and OY respectively are established. The simplified ratio ZP:ZR is (5a - 12b) : (8a + 3b).

In the parallelogram OXYZ, let's denote the point P on OX such that OP:PX = 1:2, and the point R on OY such that OR:RY = 1:3.

1. Express OP and PX in terms of a:

`OP = (1)/(3) \cdot a (since \(OP:PX = 1:2\))`

`PX = (2)/(3) \cdot a`

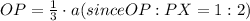
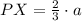
2. Express OR and RY in terms of b:

`OR = (1)/(4) \cdot b (since \(OR:RY = 1:3\))`

`RY = (3)/(4) \cdot b`

Now, we want to find the ratio ZP:ZR, where Z is the intersection of PR and QY.

ZP = OP - OZ

ZR = RY - OZ

3. Express OZ in terms of a and b:

`OZ = OY - YZ = b - (2)/(3) \cdot a (since \(OY = b\) and \(YZ = (2)/(3) \cdot a\))`

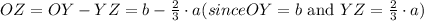
Now, substitute these values into ZP and ZR:

`ZP = (1)/(3) \cdot a - (b - (2)/(3) \cdot a)`

`\[ ZR = (3)/(4) \cdot b - (b - (2)/(3) \cdot a) \]`

4. Simplify the expressions:

`ZP = (5)/(3) \cdot a - b`

`ZR = (2)/(3) \cdot a + (1)/(4) \cdot b`

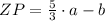
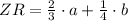
5. Find the ratio ZP:ZR:

`ZP:ZR = ((5)/(3) \cdot a - b) : ((2)/(3) \cdot a + (1)/(4) \cdot b)`

So, the simplified ratio ZP:ZR is (5a - 12b) : (8a + 3b).