Answer:

Explanation:
Let the triangle be ABC where
AB = c = 5
BC = a = 8
AC = b = 7
To find:
 Using Law of cosine
Using Law of cosine
Solution:
The Law of Cosines is a trigonometric formula used to find the measure of an angle in a triangle when the lengths of all three sides are known. The formula is given by:
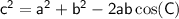
where:
-
 is the length of the side opposite angle
is the length of the side opposite angle
 ,
,
-
 and
and
 are the lengths of the other two sides.
are the lengths of the other two sides.
In this case, we want to find angle
 , and we know the lengths of the sides opposite angles
, and we know the lengths of the sides opposite angles
 ,
,
 , and
, and
 as
as
 ,
,
 , and
, and
 .
.
The Law of Cosines formula becomes:

Solving for
 :
:

Combine like terms:
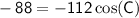
Now, solve for
 :
:
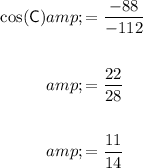
Now, find the angle
 by taking the arccosine (inverse cosine) of
by taking the arccosine (inverse cosine) of
 :
:
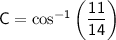
Using a calculator to find the numerical value of
 .
.
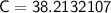
The result is approximately
 in nearest tenth
in nearest tenth
So,
