Question

During the economic downturn in 2008, the price of a stock, A(x), over an 18-month period decreased and then

increased according to the equation A(x) = 0.70x2 - 6x + 15, where x equals the number of months. The price of
another stock, B(x), increased according to the equation B(x) = 2.75x + 1.50 over the same 18-month period. State all
prices, to the nearest dollar, when both stock values were the same.

Answer 1

(-2) + (3-7)

(-1) * (-2)

EVALUATE THE EXPRESSION

Explanation:

HELP ME PLS

Answer 2

Using the quadratic equation formula, the prices of stocks A and B were the same (to the nearest dollar) at approximately $9 and $19.

The equation for Stock A is A(x) = 0.70x2 - 6x + 15

The equation for Stock B is B(x) = 2.75x + 1.50

We set the two equations equal to each other and solve for (x):

[0.70x^2 - 6x + 15 = 2.75x + 1.50]

Rearranging the terms gives us a quadratic equation:

[0.70x^2 - 8.75x + 13.5 = 0]

Using the quadratic formula
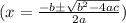`(x = (-b \pm √(b^2 - 4ac))/(2a))`, where (a = 0.70), (b = -8.75), and (c = 13.5):

`[x = (-(-8.75) \pm √((-8.75)^2 - 4 \cdot 0.70 \cdot 13.5))/(2 \cdot 0.70)]`

Solving this equation gives us two solutions for (x), which are approximately (x \approx 2.96) months and (x \approx 6.49) months.

Substituting these values into either the equation for (A(x)) or (B(x)), we find the corresponding prices:

`(x \approx 2.96) months, (A(x) \approx B(x) \approx $9)`.

`(x \approx 6.49) months, (A(x) \approx B(x) \approx $19).`

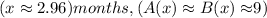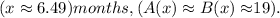
Thus, the prices of stocks A and B were the same (to the nearest dollar) at approximately $9 and $19 during the 18-month period.