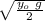Question

A ball is thrown horizontally to the right, from the top of a vertical cliff of height h. A wind blows horizontally to the left, and assume (simplistically) that the effect of the wind is to provide a constant force to the left, equal in magnitude to the weight of the ball. How fast should the ball be thrown so that it lands at the foot of the cliff

Answer 1

v =
`\sqrt{(y_o \ g)/(2) }`

Step-by-step explanation:

For this exercise we must use the projectile launch ratios, let's start by finding the time it takes to reach the bottom of the cliff, the initial vertical velocity is zero

y = y₀ +
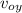`v_(oy)` t - ½ g t²

at the bottom of the cliff y = 0 and as the body is thrown horizontally the initial vertical velocity is zero

0 = y₀ + 0 - ½ g t²

t =
`√(2y_o/g)`

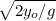
this time is the same as the horizontal movement.

Let's use Newton's second law to find the acceleration on this x-axis due to the force of the air

F = m aₓ

they tell us that force is equal to the weight of the body

-mg = maₓ

aₓ = -g

the sign indicates that the acceleration is to the left

we write the kinematics equation

x = x₀ + v₀ₓ t + ½ aₓ t²

They indicate that the final position is the foot of the cliff (x = 0), when it leaves the top it is at x₀ = 0 and has a velocity v₀ₓ = v

we substitute

0 = 0 + v t + ½ (-g) t²

v = ½ g t

we use the drop time

v = ½ g
`\sqrt{(2yo)/(g) }`

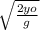
v =
`\sqrt{(y_o \ g)/(2) }`