Question

PLEASE SOLVE AND CHECK. SHOW COMPLETE SOLUTION

Answer 1

`√(4x + 13) = x + 2`

• First square both sides.

`= > ( √(4x + 13) ) ^(2) = (x + 2) ^(2)`

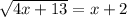
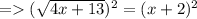
• Now, square root and square gets cancel out in the LHS. And in the RHS, apply the identity: (a + b)² = a² + 2ab + b².

`= > 4x + 13 = {(x)}^(2) + 2 * x * 2 + (2) ^(2) \\ = > 4x + 13 = {x}^(2) + 4x + 4`

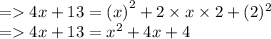
• Now, transpose 4x and 4 to LHS.

`= > 4x - 4x + 13 - 4 = {x}^(2) \\`

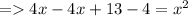
• Now, do the addition and subtraction.

`= > {x}^(2) = 9 \\ = > x = √(9) \\ = > x = ±3`

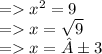
Answer:

x = ± 3

Hope you could understand.

If you have any query, feel free to ask.