Question

g In an historical movie, two knights on horseback start from rest 84.1 m apart and ride directly toward each other to do battle. Sir George's acceleration has a magnitude of 0.316 m/s2, while Sir Alfred's has a magnitude of 0.289 m/s2. Relative to Sir George's starting point, where do the knights collide?

Answer 1

The knights will collide at 43.854 meters relative to Sir George's starting point.

Step-by-step explanation:

Let suppose that initial positions of Sir George and Sir Alfred are 0 and 84.1 meters, respectively. If both knights accelerate uniformly, then we have the following kinematic formulas:

Sir George

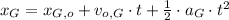`x_(G) = x_(G,o)+v_(o,G)\cdot t + (1)/(2)\cdot a_(G)\cdot t^(2)` (1)

Sir Alfred

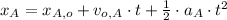`x_(A) = x_(A,o)+v_(o,A)\cdot t + (1)/(2)\cdot a_(A)\cdot t^(2)` (2)

Where:

`x_(G,o)`,
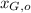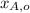`x_(A,o )` - Initial position of Sir George and Sir Alfred, measured in meters.

`x_(G)`,
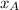`x_(A)` - Final position of Sir George and Sir Alfred, measured in meters.

`v_(o,G)`,
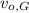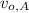`v_(o,A)` - Initial velocity of Sir George and Sir Alfred, measured in meters per second.

`t` - Time, measured in seconds.

`a_(G)`,
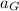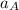`a_(A)` - Acceleration of Sir George and Sir Alfred, measured in meters per square second.

Both knights collide when
`x_(G) = x_(A)`, then we simplify this system of equations below:

`x_(G,o) + v_(o,G)\cdot t + (1)/(2)\cdot a_(G)\cdot t^(2) = x_(A,o)+v_(o,A)\cdot t + (1)/(2)\cdot a_(A)\cdot t^(2)`

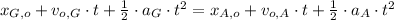
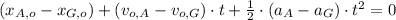`(x_(A,o)-x_(G,o)) +(v_(o,A)-v_(o,G))\cdot t +(1)/(2)\cdot (a_(A)-a_(G))\cdot t^(2) = 0` (3)

If we know that
`x_(A,o) = 84.1\,m`,
`x_(G,o) = 0\,m`,
`v_(o,A) = 0\,(m)/(s)`,
`v_(o,G) = 0\,(m)/(s)`,
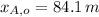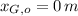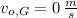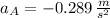`a_(A) = -0.289\,(m)/(s^(2))` and
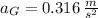`a_(G) = 0.316\,(m)/(s^(2))`, then we have the following formula:

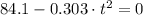`84.1 -0.303\cdot t^(2) = 0` (4)

The time associated with collision is:

`t \approx 16.660\,s`

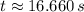
And the point of collision is:

`x_(G) = 0\,m + \left(0\,(m)/(s) \right)\cdot (16.660\,s)+ (1)/(2)\cdot \left(0.316\,(m)/(s^(2)) \right) \cdot (16.660\,s)^(2)`

`x_(G) = 43.854\,m`

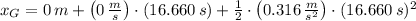
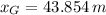
The knights will collide at 43.854 meters relative to Sir George's starting point.