Question

PLEASE HELP!! 100 POINTS!!!

petri dish of bacteria was first counted to have 150 specimen. After 4 days, the number of specimen was counted to be 450. At the same time, the bacteria appeared to be growing at an exponential rate.

1. How long would it take for the petri dish to be filled with 2000 specimen?

Round your answer to the nearest tenth.​

Answer 1

9.4 days

Explanation:

To determine how long it would take for the petri dish to be filled with 2000 specimens, we can use the general form of an exponential function:

`\large\boxed{f(t)=Ae^(kt)}`

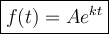
where:

• f(t) is the value at time t.
• A is the initial value.
• k is the growth/decay rate.
• t is time.

In this case, the initial number of bacteria is 150, so A = 150.

`f(t)=150e^(kt)`

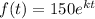
Given that the population of bacteria is 450 after 4 days, can substitute f(t) = 450 and t = 4 into the function to determine the value of k:

`450=150e^(4k)`

`(450)/(150)=(150e^(4k))/(150)`

`3=e^(4k)`

`\ln(3)=\ln\left(e^(4k)\right)`

`\ln(3)=4k\ln(e)`

`4k=\ln(3)`

`k=(\ln(3))/(4)`

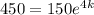
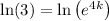
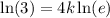
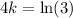
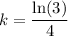
Therefore, the exponential function that models the given information is:

`\Large\boxed{\boxed{f(t)=150e^{(t\ln(3))/(4)}}}`

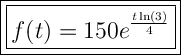
To find how long would it take for the petri dish to be filled with 2000 specimen, set f(t) = 2000 and solve for t:

`150e^{(t\ln(3))/(4)}=2000`

`\frac{150e^{(t\ln(3))/(4)}}{150}=(2000)/(150)`

`e^{(t\ln(3))/(4)}=(40)/(3)`

`\ln\left(e^{(t\ln(3))/(4)}\right)=\ln\left((40)/(3)\right)`

`(t\ln(3))/(4)\ln(e)=\ln\left((40)/(3)\right)`

`(t\ln(3))/(4)=\ln\left((40)/(3)\right)`

`t\ln(3)=4\ln\left((40)/(3)\right)`

`t=(4\ln\left((40)/(3)\right))/(\ln(3))`

`t=9.43105112...`

`t=9.4\; \sf days\;(nearest\;tenth)`

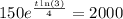
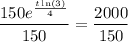
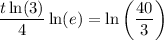
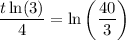
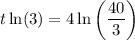
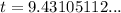
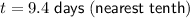
Therefore, it would take 9.4 days for the petri dish to be filled with 2000 specimen.