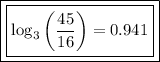Question

PLEASE HELP ME!!!! 100 POINTS!!!!

Given 5 ≈1.465 and 16 ≈2.524, evaluate the expressions. Note: you must use the given values and not values obtained from a calculator for those logarithms. 4 4516 (picture below for reference)​

Answer 1

log(5)/log(3) = 1.465

log(16)/log(3) = 2.524

(a) log(4)/log(3) = log(√16)/log(3)

= (1/2)log(16)/log(3)

= (1/2)(2.524) = 1.262

(b) log(45/16)/log(3)

= (log(45) - log(16))/log(3)

= (log(3² × 5) - log(16))/log(3)

= (2log(3) + log(5) - log(16))/log(3)

= 2 + (log(5)/log(3)) - (log(16)/log(3))

= 2 + 1.465 - 2.524

= .941

Answer 2

`\textsf{(a)} \quad \log_34=1.262`

`\textsf{(c)}\quad \log_3\left((45)/(16)\right)=0.941`

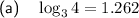
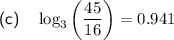
Explanation:

Given logarithmic approximations:

`\log_35 \approx 1.465`

`\log_316\approx 2.524`

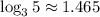
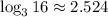
To use these values to evaluate the given expressions, we can apply the logarithmic rules:

`\boxed{\begin{array}{rl}\underline{\sf Logarithmic\;Rules}\\\\\sf Product:&\log_axy=\log_ax + \log_ay\\\\\sf Quotient:&\log_a \left((x)/(y)\right)=\log_ax - \log_ay\\\\\sf Power:&\log_ax^n=n\log_ax\\\\\end{array}}`

`\hrulefill`

Part (a)

To find log₃(4) using the given approximations, begin by recognizing that 4 is the square root of 16:

`\log_34=\log_3√(16)`

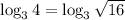
Express the square root in exponent form:

`\log_34=\log_3\left(16^(\frac12)\right)`

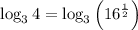
Now, use the power rule for logarithms:

`\log_34=(1)/(2)\log_316`

Finally, substitute the given value of log₃18 ≈ 2.524 into the equation to evaluate log₃4:

`\log_34=(1)/(2)\cdot 2.524`

`\boxed{\boxed{\log_34=1.262}}`

`\hrulefill`

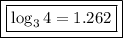
Part (c)

To evaluate log₃(45/16), begin by applying the quotient rule for logarithms:

`\log_3\left((45)/(16)\right)=\log_345-\log_316`

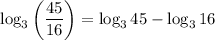
Now, rewrite 45 as the product of 9 and 5:

`\log_3\left((45)/(16)\right)=\log_3(9 \cdot 5)-\log_316`

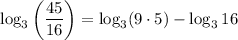
Apply the product rule for logarithms:

`\log_3\left((45)/(16)\right)=\log_39+\log_35-\log_316`

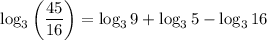
Rewrite 9 as 3²:

`\log_3\left((45)/(16)\right)=\log_3\left(3^2\right)+\log_35-\log_316`

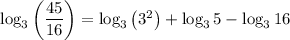
Use the power rule for logarithms:

`\log_3\left((45)/(16)\right)=2\log_33+\log_35-\log_316`

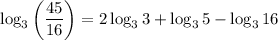
Now, apply the logarithmic rule logₐ(a) = 1:

`\log_3\left((45)/(16)\right)=2(1)+\log_35-\log_316`

`\log_3\left((45)/(16)\right)=2+\log_35-\log_316`

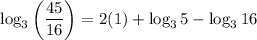
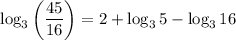
Finally, substitute the given values of log₃5 ≈ 1.465 and log₃16 ≈ 2.524 into the equation to evaluate log₃(45/16):

`\log_3\left((45)/(16)\right)=2+1.465-2.524`

`\boxed{\boxed{\log_3\left((45)/(16)\right)=0.941}}`