Answer:
the number density of the protons in the beam is 3.2 × 10¹³ m⁻³
Step-by-step explanation:
Given that;
diameter D = 2.0 mm
current I = 1.0 mA
K.E of each proton is 20 MeV
the number density of the protons in the beam = ?
Now, we make use of the relation between current and drift velocity
I = MeAv ⇒ 1 / eAv
The kinetic energy of protons is given by;
K =

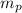 v²
v²
v = √( 2K /
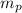 )
)
lets relate the cross-sectional area A of the beam to its diameter D;
A =
 πD²
πD²
now, we substitute for v and A
n = I /
 πeD² ×√( 2K /
πeD² ×√( 2K /
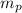 )
)
n = 4I/π eD² × √(
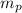 / 2K )
/ 2K )
so we plug in our values;
n = ((4×1.0 mA)/(π(1.602×10⁻¹⁹C)(2mm)²) × √(1.673×10⁻²⁷kg / 2×( 20 MeV)(1.602×10⁻¹⁹ J/ev )
n = 1.98695 × 10¹⁸ × 1.6157967 × 10⁻⁵
n = 3.2 × 10¹³ m⁻³
Therefore, the number density of the protons in the beam is 3.2 × 10¹³ m⁻³