Question

Danny flies a drone in a circular path around an object that is 210 feet west and 220 feet south of his position. The drone's path takes it over a point that is 160 feet east and 160 feet south of him. Find an equation for the drone's path. (Assume Danny is located at the origin, with the horizontal axis running east-west and the vertical axis running north-south)

Answer 1

The answer is below

Explanation:

A circle is the locus of a points such that its distance from a fixed point is always constant.

Since the drone moves in a circular path, therefore the path of the drone forms a circle. The equation of a circle is given by:

(x - h)² + (y - k)² = r²; where (h, k) is the center of the circle and r is the radius of the circle.

Danny is located at the origin. Since the drone flies in a circular path around an object that is 210 feet west and 220 feet south of his position. Hence the center of the circular path is (-210, -220).

Also, the drone's path takes it over a point that is 160 feet east and 160 feet south of him i.e. (160, -160). Therefore the radius of the circle is the distance between point (-210, -220) and point (160, -160)

`radius=√((160-(-210))^2+(-160-(-220))^2)=√(140500)`

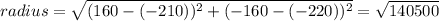
Using (x - h)² + (y - k)² = r²:

[x - (-210)]² + [y - (-220)]² = (√140500)²

(x + 210)² + (y + 220)² = 140500

x² + 420x + 44100 + y² + 440y + 48400 = 140500

x² + y² + 420x + 440y - 48000 = 0