Answer:
Angle between the diagonal of a cube of side length 8 and the diagonal of one of its faces is equal to
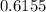 radian
radian
Explanation:
Please see the attached image for better understanding
Length of OB is equal to
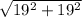
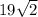
Now the length of OE is equal to
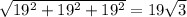
Now Angle BOE is equal to
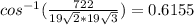 radians
radians
Angle between the diagonal of a cube of side length 8 and the diagonal of one of its faces is equal to
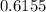 radian
radian