Question

Calculate the magnitude and direction of the Coulomb force on each of the three charges shown in the figure below

Answer 1

The Coulomb forces between the charges are approximately 90 N (attractive), 225 N (repulsive), and 43.2 N (attractive) for the respective pairs of charges.

Let's calculate the magnitudes of the Coulomb forces using Coulomb's Law for each pair of charges.

`\[ F_1 = k (q_1 q_2)/(r_1^2) \]\[ F_1 = (8.99 * 10^9 \ \text{N m}^2/\text{C}^2) \frac{(6.00 * 10^(-6) \ \text{C})(1.50 * 10^(-6) \ \text{C})}{(0.03 \ \text{m})^2} \]`

`\[ F_1 \approx 90 \ \text{N} \]`

Now, for the second pair of charges:

`\(q_1 = 1.50 \ \mu C\)\\ \(q_2 = -2.00 \ \mu C\)\\ \(r_2 = 2 \ \text{cm} = 0.02 \ \text{m}\)`

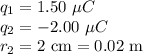
`\[ F_2 = k (q_1 q_2)/(r_2^2) \]\[ F_2 = (8.99 * 10^9 \ \text{N m}^2/\text{C}^2) \frac{(1.50 * 10^(-6) \ \text{C})(-2.00 * 10^(-6) \ \text{C})}{(0.02 \ \text{m})^2} \]`

Calculating
`\(F_2\)`:

`\[ F_2 \approx -225 \ \text{N} \]`

Finally, for the third pair of charges:

`\(q_1 = 6.00 \ \mu C\)\\\(q_2 = -2.00 \ \mu C\)\\\(r_3 = 5 \ \text{cm} = 0.05 \ \text{m}\)`

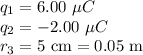
`\[ F_3 = k (q_1 q_2)/(r_3^2) \]\[ F_3 = (8.99 * 10^9 \ \text{N m}^2/\text{C}^2) \frac{(6.00 * 10^(-6) \ \text{C})(-2.00 * 10^(-6) \ \text{C})}{(0.05 \ \text{m})^2} \]`

`\(F_3\):\[ F_3 \approx -43.2 \ \text{N} \]`

So, the magnitudes of the Coulomb forces are approximately:

`\(F_1 \approx 90 \ \text{N}\)\\\\ \(F_2 \approx 225 \ \text{N}\)\\ \\\(F_3 \approx 43.2 \ \text{N}\)`

The direction of the force is attractive if the charges have opposite signs (as in
`\(F_1\)` and
`\(F_3\))`, and repulsive if they have the same sign (as in
`\(F_2\))`.