Question

A marble on a frictionless track, starting from point A in the drawing, is projected down the curved runway. (This means that the initial speed of the particle is NOT zero!) Upon leaving the runway at point B, the particle is traveling straight upward and reaches a height of 5.00 m above the floor before falling back down. Ignoring air resistance, find the initial speed of the particle (v0) at point A.

Answer 1

v = 4.4 m / s

Step-by-step explanation:

Unfortunately, the exercise scheme does not appear. Let's analyze the problem the marble leaves point A with an initial velocity, goes down and then rises to a given height where its velocity is zero, in the whole trajectory they tell us that the resistance is zero, so we can use the conservation relations of the enegy.

Starting point. Point A

Em₀ = K + U = ½ m v2 + mg y_a

point B.

Em_f = U = m g y

the energy is conserved

Em₀ = Em_f

½ m v² + mg y_a = m g y

½ m v² = m g (y -y_a)

v =
`\sqrt {2g ( y - y_a)}`

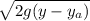
In the exercise the diagram is not seen, but the height of point A must be known, suppose that y_a = 4 m

v =
`√( 2 \ 9.8 ( 5 -4))`

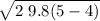
v = 4.4 m / s