⭐ Let "a" be the cost of each kg of apples and "o" be the cost of each kg of oranges.
⭐ First of all understanding all the question carefully, we can form two equation which can be given by,
(Total cost of 3kg apple and 5kg oranges is total about 1080Rs.)
(Cost of 3kg of apples is equal as the same cost of 7kg of oranges)
Now we can substitute the value of (7o) instead of (3a) so as to collect the same variables. Substituting values,
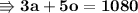
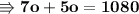
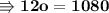
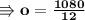
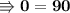
Now replacing value of (o = 90) in equation (2),
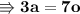
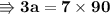
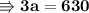
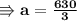
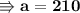
- Thus the values of each kg of apples are 210Kg and of oranges are 90Kg