Question

I need help with this problem

Answer 1

The 90% confidence interval for students sharing a ride (2.505, 4.095) and the 95% interval (2.308, 4.292) both include.

Part A:

Parameters and Conditions

Parameter: Mean number of students who share a ride to school.

Conditions for Confidence Intervals:

Random Sampling: It's mentioned that simple random sampling of 20 students was conducted from a population of 300 students. Independence: Each student's choice to share a ride should not be influenced by others. This assumption might hold true unless there are specific constraints or social factors impacting ride-sharing.

Part B:

Construction of Confidence Intervals

Let's start by finding the sample mean
`(\(\bar{x}\))` and sample standard deviation
`(\(s\))` from the collected data:

Data:

`\(6555323622\)`

`\(5433425345\)`

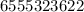
Sample Mean
`(\(\bar{x}\)):`

`\((6+5+5+5+3+2+3+6+2+2+5+4+3+4+2+5)/(20) = (66)/(20) = 3.3\)`

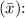
Sample Standard Deviation
`(\(s\))` :

`\(s = \sqrt{\frac{\sum(x - \bar{x})^2}{n - 1}}\)`

`\(s = \sqrt{((6-3.3)^2 + (5-3.3)^2 + ... + (5-3.3)^2)/(19)}\)`

`\(s = \sqrt{(14.89 + 3.61 + ... + 3.61)/(19)}\)`

`\(s = \sqrt{(80.4)/(19)} \approx √(4.23) \approx 2.06\)`

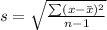
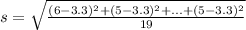
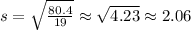
90% Confidence Interval:

For a 90% confidence interval with a t-distribution:

Degrees of Freedom
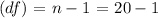`(\(df\)) = \(n - 1\) = \(20 - 1\)` = 19

Critical Value
`(\(t\))` for 90% confidence level and 19 degrees of freedom = ±1.729 (obtained from a t-table)

Margin of Error
`(\(ME_(90)\))` =
`\(t * (s)/(√(n))\)`

`\(ME_(90) = 1.729 * (2.06)/(√(20)) \approx 0.795\)`

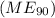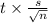
Confidence Interval:

`\(\bar{x} \pm ME_(90) = 3.3 \pm 0.795 = (2.505, 4.095)\)`

95% Confidence Interval:

For a 95% confidence interval with a t-distribution:

Critical Value
`(\(t\))` for 95% confidence level and 19 degrees of freedom = ±2.093 (obtained from a t-table)

Margin of Error
`(\(ME_(95)\))` =
`\(t * (s)/(√(n))\)`

`\(ME_(95) = 2.093 * (2.06)/(√(20)) \approx 0.992\)`

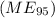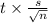
Confidence Interval:

`\(\bar{x} \pm ME_(95) = 3.3 \pm 0.992 = (2.308, 4.292)\)`

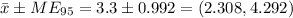
Part C:

Interpretation and Comparison

90% Confidence Interval: We are 90% confident that the true mean number of students who share a ride to school is between 2.505 and 4.095.

95% Confidence Interval: We are 95% confident that the true mean number of students who share a ride to school is between 2.308 and 4.292.

Part D:

Based on the findings, it seems likely that the mean number of students sharing a ride to school is between approximately 2 and 4. Since the condition set for developing the ride-sharing app was if more than three students share a ride on average.