Answer:
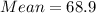
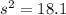 --- Variance
--- Variance
Explanation:
Given
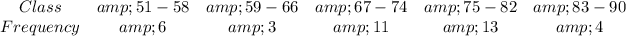
Solving (a): Calculate the mean.
The given data is a grouped data. So, first we calculate the class midpoint (x)
For 51 - 58.
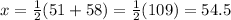
For 59 - 66
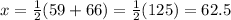
For 67 - 74

For 75 - 82
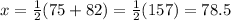
For 83 - 90
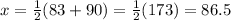
So, the table becomes:
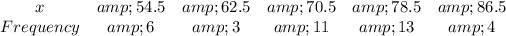
The mean is then calculated as:
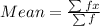
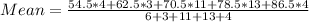
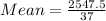
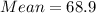 -- approximated
-- approximated
Solving (b): The sample variance:
This is calculated as:
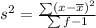
So, we have:


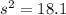 -- approximated
-- approximated