Question

HELP ME 100 POINTS!!

Select all of the rational numbers.
!SELECT TWO ANSWERS!
Question 2 options:

0.15783456

-200

4 1/9

0.23--

Answer 1

`\boxed{\checkmark}\;\;0.15783456`

`\boxed{\phantom{\checkmark}}\;\;-√(200)`

`\boxed{\checkmark}\;\;4(1)/(9)`

`\boxed{\checkmark}\;\;0.\overline{23}`

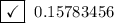
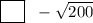
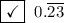
Explanation:

A rational number is any number that can be expressed as the quotient or fraction of two integers, where the denominator is not zero.

`\hrulefill`

0.15783456 is a finite decimal.

Finite decimals can be expressed as a fraction by multiplying and dividing the number by a power of 10 that corresponds to the number of decimal places. So in this case, there are 8 digits after the decimal place, so multiply and divide 0.15783456 by 10⁸ = 100,000,000:

`0.15783456* (100\:000\:000)/(100\:000\:000)=(15\:783\:456)/(100\:000\:000)`

Therefore, 0.15783456 is a rational number.

`\hrulefill`

We can rewrite 200 as the product of 10² and 2. Therefore:

`\begin{aligned}-√(200)&=-√(10^2 * 2)\\&=-√(10^2) √(2)\\&=-10√(2)\end{aligned}`

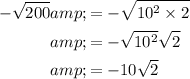
√2 is an irrational number as it cannot be expressed as a fraction. Therefore, -√(200) is also an irrational number.

`\hrulefill`

4¹/₉ is a mixed number, consisting of an integer and a fraction. Mixed numbers can be expressed an improper fractions:

`4(1)/(9)=4+(1)/(9)=(36)/(9)+(1)/(9)=(36+1)/(9)=(37)/(9)`

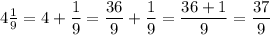
Therefore, 4¹/₉ is a rational number.

`\hrulefill`

`0.\overline{23}` is a repeating decimal. Repeating decimals can be expressed as fractions. Let x equal the repeating decimal, multiply both sides by 10, then subtract:

`\begin{aligned}x&=0.232323...\\100x&=100 * 0.232323...\\100x&=23.232323...\\\\100x-x&=23.232323...-0.232323...\\99x&=23\\\\x&=(23)/(99)\end{aligned}`

Therefore,
`0.\overline{23}` can be expressed as 23/99, so it is a rational number.