Question

A certain green light bulb emits at a single wavelength of 550 nm. It consumes 55 W of electrical power and is 75% efficient in converting electrical energy into light. (a) How many photons does the bulb emit in one hour? (b) Assuming the emitted photons to be distributed uniformly in space, how many photons per second strike a 10 cm by 10 cm paper held facing the bulb at a distance of 1.0 m?

Answer 1

a) #_total = 4 10²³ photons / h, b) # _photon_area = 3 10²² photons

Step-by-step explanation:

a) Let's start by calculating the energy of an emitted photon

E₀ = h f

c = λ f

substituting

E₀ = h c /λ

E₀ =
`(6.62 \ 10^(-34) \ 3 \ 10^(8) )/(550 \ 10^(9) )`

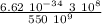
E₀ = 3.6 10⁻¹⁹ J

Let's use a direct proportion rule (res rule) if a photon has Eo, how many photons are there in 55W

#_foton = 55 / E₀

# _photon = 55 / 3.6 10⁻¹⁹ = 15.27 10¹⁹ photons

This version is with 100% if the conversion is 75%, how many footnes are there

#_foton_real = # _foton 75/100

#real_photon = 15.27 10¹⁹ 0.75

# _real_photon = 11.45 10¹⁹ photons

this is the broadcast in a second

#_total = # _real_photon t

#_total = 11.45 10¹⁹ 3600

#_total = 4.1 10²³ photons / h

#_total = 4 10²³ photons / h

b) This number of photons is constant, so after being emitted they are distributed on the surface of a sphere, in this case of radius r = 1.0 m

the volume of a sphere is

A = 4π r²

A = 4π 1²

A = 12,566 m²

the area of ​​the plate is

A₁ = l₁ l₂

A₁ = 0.10 0.10

A₁ = 1 10⁻² m

Let's use a direct proportion rule, if there are 4.1 10²³ photons in an area A, how much are there in an area A₁

# _photon_area = #_total A₁ / A

# _photon_area =
`4.1 \ 10^(23) \ (1 \ 10^(-2) )/(12.566)`

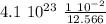
# _photon_area = 3.26 10²²

as the number of photons must be a whole number

# _photon_area = 3 10²² photons